算法与数据结构(C++)

C++基础

语法

辅助工具

生成随机数组

1
2
3
4
5
6
7
8
9
10
11
// 生成有n个元素的随机数组,每个元素的随机范围为[rangeL, rangeR]
int *generateRandomArray(int n, int rangeL, int rangeR) {

    assert(rangeL <= rangeR);

    int *arr = new int[n];

    srand(time(NULL));
    for (int i = 0; i < n; i++)
        arr[i] = rand() % (rangeR - rangeL + 1) + rangeL;
    return arr;

算法-排序

快速排序

归并排序

层级：logN , 每次归并: N

总体：NlogN

会开辟一段临时空间，O(n)的额外空间。

用空间换时间

归并过程：三个索引（要定义清楚哦 要维护定义！这真的很重要）

以下实现，数组是前闭后闭的

左边位置：left；中间：middle；右边：right

三个索引：i，j，k

堆排序

主要应用：优先队列

优先队列主要处理需要动态排序的情况。

一些静态情况也适用优先队列：

N个元素中选出前M个元素

排序：NlogN

优先队列：NlogM

优先队列的实现
主要操作 入队 出队
普通数组 O(1) O(n)
顺序数组 O(n) O(1)
堆 O(lgn) O(lgn)

对于总共N个请求

使用普通数组或顺序数组，最差情况：O(n^2)

使用堆：O(nlgn)

二叉堆的实现

要求：堆中某个节点的值总是不大于其父节点的值（最大堆；任一子节点<父节点）；堆是一棵完全二叉树（除了最后一层节点，其他层节点数必须为其能达到的最大值，最后一层的所有节点必须集中在左侧）。

用数组存储二叉堆：

子左节点序号 = 父节点序号*2;

子右节点序号 = 父节点序号*2 + 1;

0号索引一般不使用。

算法-复杂度分析

初识

n：数据规模

tips:

O(AlgA+A) = O(AlgA)

O(AlgA+B) ≠ O(AlgA)

例题：

image-20210410165908482
image-20210410165908482

image-20210410170028346
image-20210410170028346

对于已经排序好的数组，插入排序的时间复杂度：O(n)

image-20210410170417761
image-20210410170417761

对数据规模有个概念

时间复杂度

1s之内解决问题：O(n^2)的算法大概可以处理10^4级别的数据

1s之内解决问题：O(n)的算法大概可以处理10^8级别的数据

1s之内解决问题：O(NlogN)的算法大概可以处理10^7级别的数据

空间复杂度：

多开一个辅助的数组O(n)

多开一个辅助的二维数组O(n^2)

多开常数空间O(1)

递归调用是用空间代价的

递归空间复杂度=递归深度

image-20210410181502907
image-20210410181502907

简单案例

image-20210410182128415
image-20210410182128415

主要看循环数与数据规模是否呈比例 又是什么比例（正相关or？）

image-20210410182904634
image-20210410182904634

image-20210410183037969
image-20210410183037969

整型转字符串：n经过几次“除以10”操作后，等于0（仅适用于正整数）

image-20210410183202255

image-20210410183707223

image-20210410183640766

image-20210410183202255

image-20210410183707223

image-20210410183640766

判断一个数是不是素数: (没考虑负数情况 代码待优化)

image-20210411133313279
image-20210411133313279

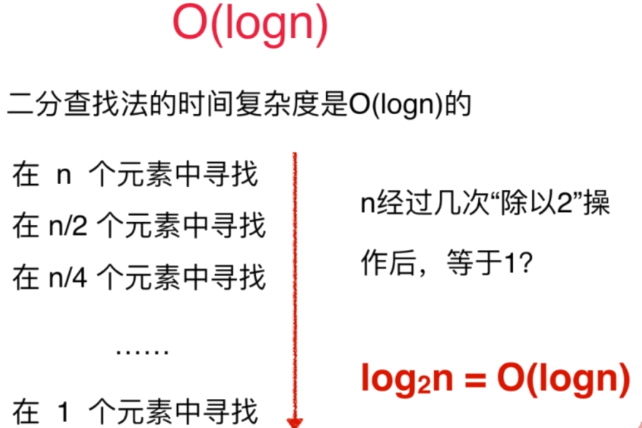
O(logN)

1
2
3
4
5
int i = 1;
while(i<n)
{
    i = i * 2;
}

O(NlogN)

1
2
3
4
5
6
7
8
for(m=1; m<n; m++)
{
    i = 1;
    while(i<n)
    {
        i = i * 2;
    }
}

O(N^2)

1
2
3
4
5
6
7
8
for(x=1; i<=n; x++)
{
   for(i=1; i<=n; i++)
    {
       j = i;
       j++;
    }
}

分析表

源：https://www.bigocheatsheet.com/

img

img

img

img

img

自测

算法-数组

算法-动态规划(DP)

简介

递归问题->重叠子问题->记忆化搜索（自顶向下地解决问题）

递归问题->重叠子问题->动态规划（自底向上地解决问题）

动态规划（英语：Dynamic programming，简称 DP）是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。

动态规划不是某一种具体的算法，而是一种算法思想：若要解一个给定问题，我们需要解其不同部分（即子问题），再根据子问题的解以得出原问题的解。

应用这种算法思想解决问题的可行性，对子问题与原问题的关系，以及子问题之间的关系这两方面有一些要求，它们分别对应了最优子结构和重复子问题。

最优子结构：规定的是子问题与原问题的关系

重复子问题：规定的是子问题与子问题的关系。

解决动态规划问题的核心：找出子问题及其子问题与原问题的关系

找到了子问题以及子问题与原问题的关系，就可以递归地求解子问题了。但重叠的子问题使得直接递归会有很多重复计算，于是就想到记忆化递归法：若能事先确定子问题的范围就可以建表存储子问题的答案。

动态规划算法中关于最优子结构和重复子问题的理解的关键点：

证明问题的方案中包含一种选择，选择之后留下一个或多个子问题
设计子问题的递归描述方式
证明对原问题的最优解包括了对所有子问题的最优解
证明子问题是重叠的（这一步不是动态规划正确性必需的，但是如果子问题无重叠，则效率与一般递归是相同的）

基础

斐波那契递归优化

优化前
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <iostream>
#include <ctime>

using namespace std;

int num = 0;
// 递归求斐波那契数列
int fib( int n ){

    num ++;

    if( n == 0 )
        return 0;

    if( n == 1 )
        return 1;

    return fib(n-1) + fib(n-2);
}
int main() {

    num = 0;

    int n = 42;
    time_t startTime = clock();
    int res = fib(n);
    time_t endTime = clock();

    cout << "fib(" << n << ") = " << res << endl;
    cout << "time : " << double(endTime - startTime) / CLOCKS_PER_SEC << " s" << endl;
    cout << "run function fib() " << num << " times." << endl;

    return 0;
}

output:

1
2
3
4
5
6
7
8
9
耗时：N/A
fib(42) = 267914296
time : 2.4807 s
run function fib() 866988873 times.
--
耗时：0 ms
fib(10) = 55
time : 1e-06 s
run function fib() 177 times.

时间复杂度：O(2^n)

有大量的重复运算。为了避免这一重复运算，适用动态规划。记录答案。

优化后

优化（记忆化搜索）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <iostream>
#include <ctime>
#include <vector>

using namespace std;

vector<int> memo;
int num = 0;

// 记忆化搜索
int fib(int n){

    num ++;

    if(n == 0)
        return 0;

    if(n == 1)
        return 1;

    if(memo[n] == -1)
        memo[n] = fib(n - 1) + fib(n - 2);

    return memo[n];
}

int main() {

    num = 0;

    //int n = 42;
    int n = 1000; // 注意: 我们使用n = 1000只是为了测试性能, 实际上会溢出
                  // 斐波那契额数列是以指数速度上涨的
    memo = vector<int>(n + 1, -1);

    time_t startTime = clock();
    int res = fib(n);
    time_t endTime = clock();

    cout << "fib(" << n << ") = " << res << endl;
    cout << "time : " << double(endTime - startTime) / CLOCKS_PER_SEC << " s" << endl;
    cout << "run function fib() " << num << "times." << endl;

    return 0;
}

output:

1
2
3
4
5
6
执行完成，耗时：0 msfib(10) = 55
time : 2e-06 s
run function fib() 19times.
执行完成，耗时：0 msfib(42) = 267914296
time : 3e-06 s
run function fib() 83times.

java版本：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
import java.util.Arrays;

// 记忆化搜索
public class Solution2 {

    private int num = 0;

    public int fib(int n){

        int[] memo = new int[n + 1];
        Arrays.fill(memo, -1);
        return fib(n, memo);
    }

    private int fib(int n, int[] memo){

        num ++;

        if(n == 0)
            return 0;

        if(n == 1)
            return 1;

        if(memo[n] == -1)
            memo[n] = fib(n - 1, memo) + fib(n - 2, memo);

        return memo[n];
    }

    public int getNum(){
        return num;
    }

    public static void main(String[] args) {

        //int n = 42;
        int n = 1000; // 注意: 我们使用n = 1000只是为了测试性能, 实际上会溢出
                      // 斐波那契额数列是以指数速度上涨的

        Solution2 solution = new Solution2();
        long startTime = System.currentTimeMillis();
        int res = solution.fib(n);
        long endTime = System.currentTimeMillis();

        System.out.println("fib(" + n + ") = " + res);
        System.out.println("time : " + (endTime - startTime) + " ms");
        System.out.println("run function fib() " + solution.getNum() + " times.");
    }
}

最优子结构-发现重叠子问题

对于一个递归问题，发现重叠子问题和最优子结构，才可以使用记忆化搜索/动态规划。

比如343. 整数拆分，d(n)=1*d(n-1)+2*d(n-2)+…+(n-1)*1

例题

70. 爬楼梯

动态规划最终提交（java）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int climbStairs(int n) {
        int[] memo = new int[n+1];

        if(n==0){return 1;}
        if(n==1){return 1;}
        if(n==2){return 2;}

        memo[0]=1;
        memo[1]=1;
        memo[2]=2;

        for(int i=2;i<=n;i++){
            memo[i] = memo[i-1]+memo[i-2];
        }

        return memo[n];
    }
}

数学鬼才踢脚板：

1
2
3
4
5
6
7
class Solution {
    public int climbStairs(int n) {
        double sqrt_5 = Math.sqrt(5);
        double fib_n = Math.pow((1 + sqrt_5) / 2, n + 1) - Math.pow((1 - sqrt_5) / 2,n + 1);
        return (int)(fib_n / sqrt_5);
    }
}

？矩阵快速幂有必要吗有必要吗有必要吗？？？：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public class Solution {
    public int climbStairs(int n) {
        int[][] q = {{1, 1}, {1, 0}};
        int[][] res = pow(q, n);
        return res[0][0];
    }

    public int[][] pow(int[][] a, int n) {
        int[][] ret = {{1, 0}, {0, 1}};
        while (n > 0) {
            if ((n & 1) == 1) {
                ret = multiply(ret, a);
            }
            n >>= 1;
            a = multiply(a, a);
        }
        return ret;
    }

    public int[][] multiply(int[][] a, int[][] b) {
        int[][] c = new int[2][2];
        for (int i = 0; i < 2; i++) {
            for (int j = 0; j < 2; j++) {
                c[i][j] = a[i][0] * b[0][j] + a[i][1] * b[1][j];
            }
        }
        return c;
    }
}