更新中
分钱问题 分钱问题:一个房间里有100个人,每个人有100美元。每隔一定时间(比如1秒),每个有钱的人都会给随机选择的一个人一美元。经过一段时间的进展,这些钱将如何分配?
The post Counterintuitive problem: Everyone in a room keeps giving dollars to random others. You’ll never guess what happens next. appeared first on Decision Science News .
程序模拟结果:
核心代码:
1 2 3 4 5 6 7 8 9 10 //delay一定时间 //... //数据处理 for(int i = 0 ; i < money.length; i ++){ int j = (int)(Math.random() * money.length); money[i] -= 1; money[j] += 1; } //数据显示于屏幕 //...
这样一个混沌体系,随着时间增加,最终显示的状态是非常不稳定的。
蒙特卡洛算法暴力求PI值 蒙特卡罗算法并不是一种算法的名称,而是对一类随机算法的特性的概括。
这个名称只是概括了算法的特性。与之类似的称呼还有拉斯维加斯算法。
蒙特卡罗算法:采样越多,越近似 最优解;有机会找到 最优解;
这两类随机算法之间的选择,往往受到问题的局限。如果问题要求在有限采样内,必须给出一个解,但不要求是最优解,那就要用蒙特卡罗算法。反之,如果问题要求必须给出最优解,但对采样没有限制,那就要用拉斯维加斯算法。对于机器围棋程序而言,因为每一步棋的运算时间、堆栈空间都是有限的,而且不要求最优解,所以ZEN涉及的随机算法,肯定是蒙特卡罗式的。
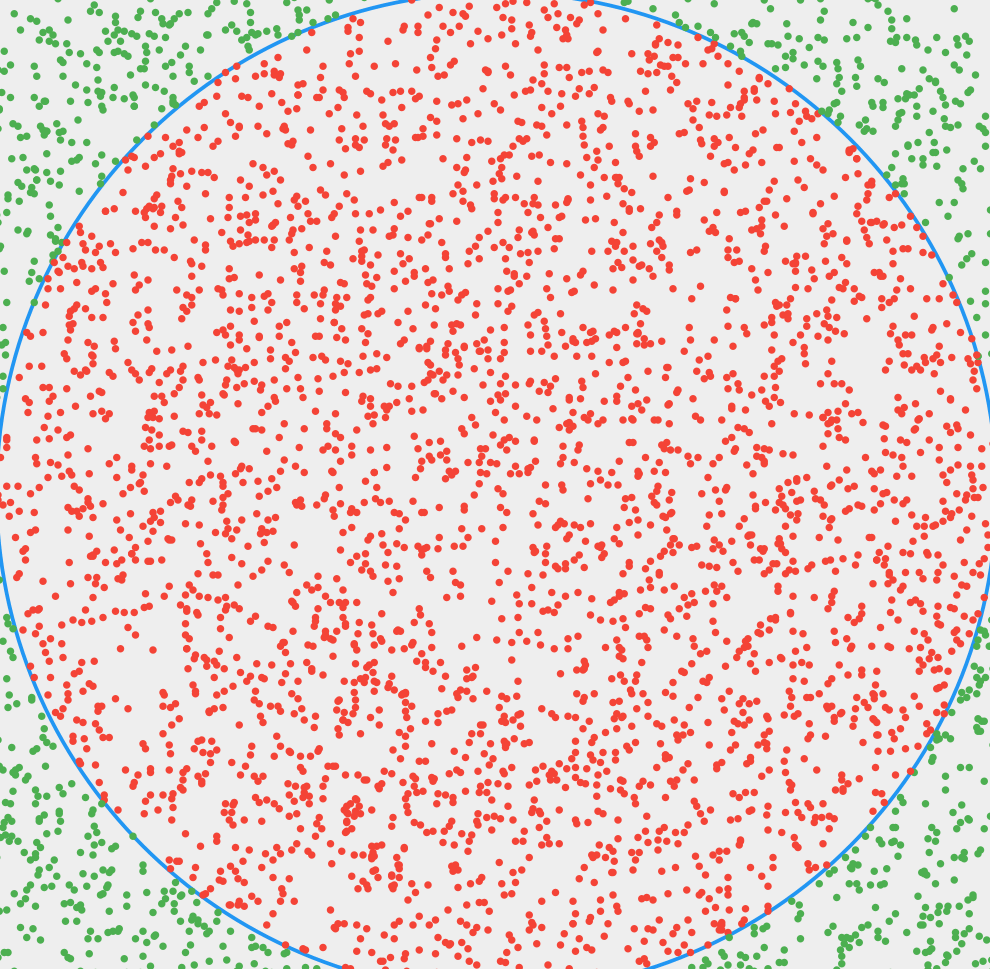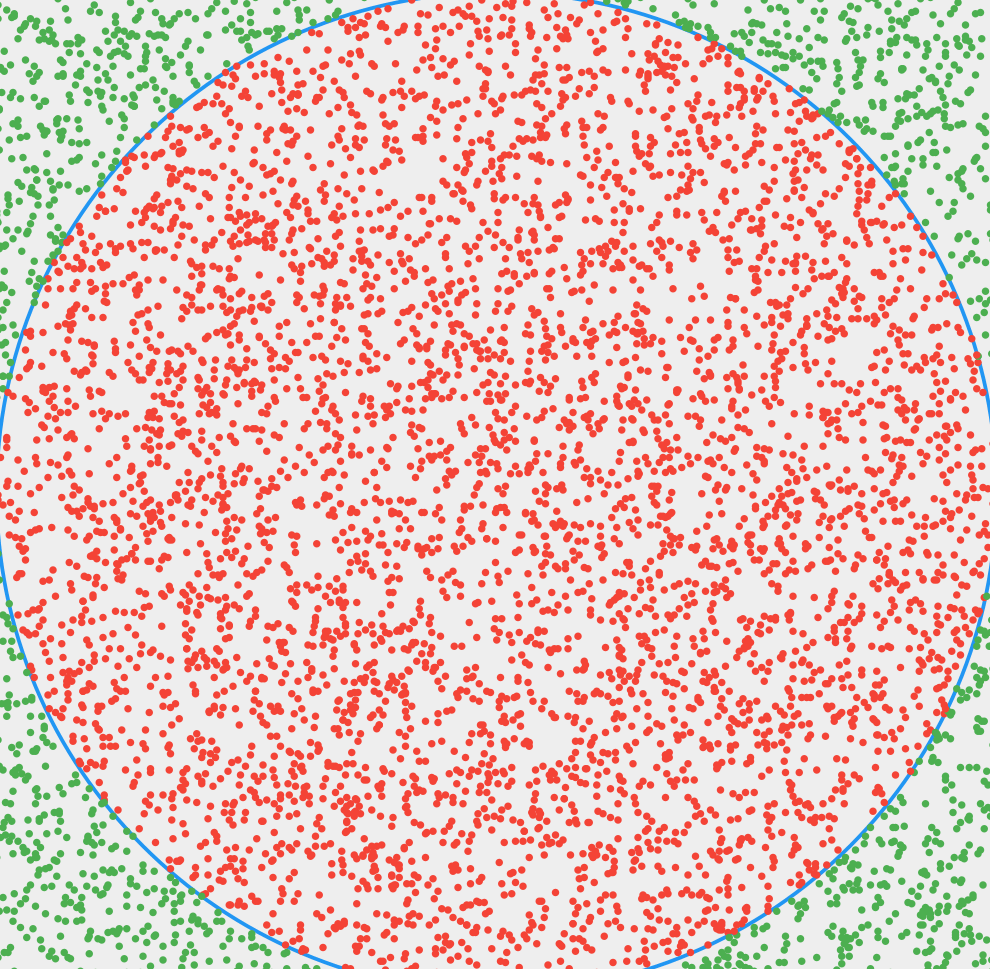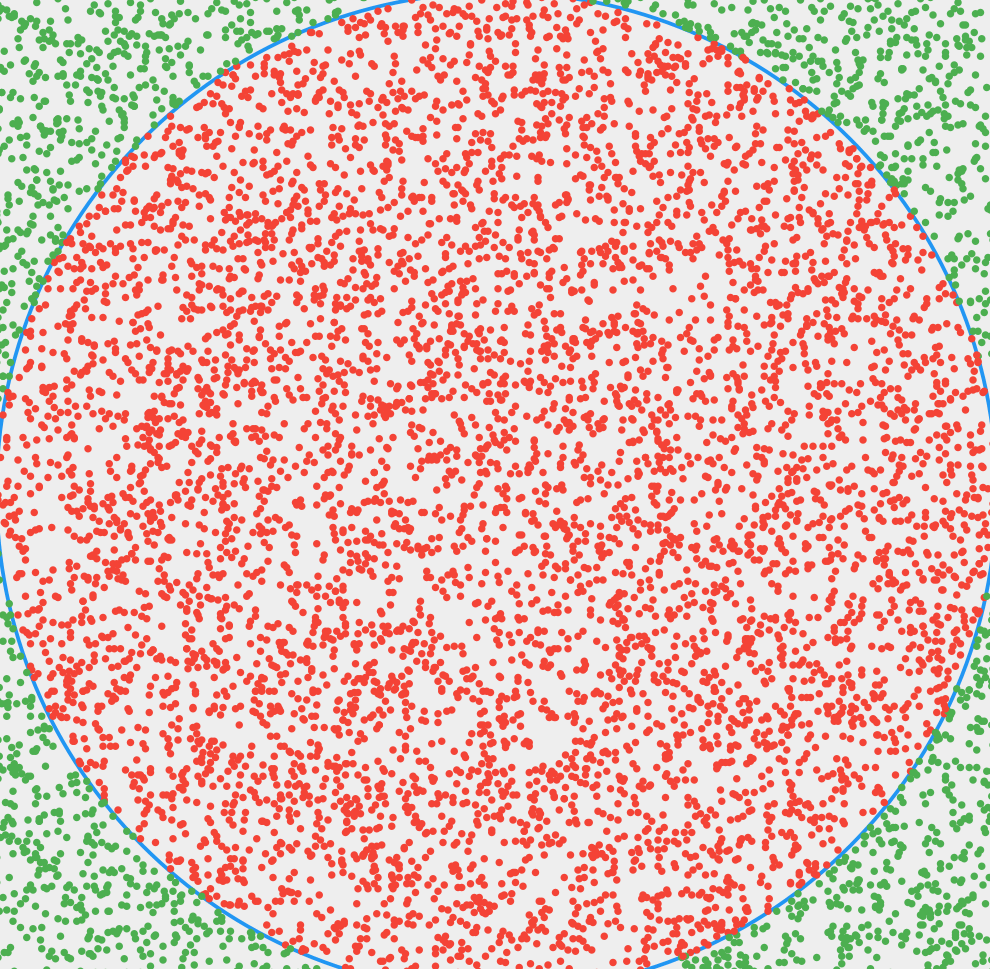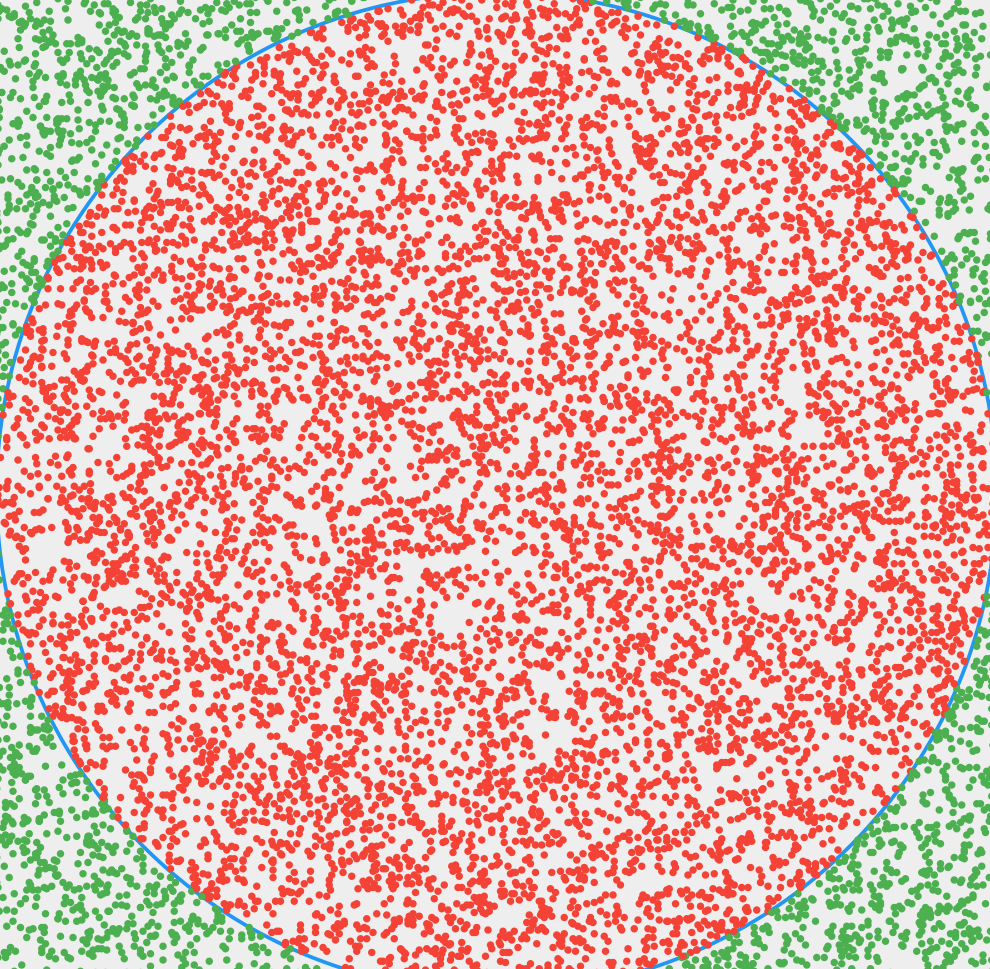
核心思想:在边长为1的正方形方框内随机抛点,统计落在圆弧内的点所占比例。随着点数量的增加,这个比例越来越接近四分之一圆面积与正方形面积之比,即为PI/4。
核心代码:
一个圆类(Model),并有计算点是否包含在其中的方法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 import java.awt.*; import javax.swing.*; public class Circle { private int x, y, r; public Circle(int x, int y, int r){ this.x = x; this.y = y; this.r = r; } public int getX(){ return x; } public int getY(){ return y; } public int getR(){ return r; } public boolean contain(Point p){ return Math.pow(p.x - x, 2) + Math.pow(p.y - y, 2) <= r*r; } }
一个另外的数据类(Model),用来记录点的相对位置,并能返回PI值:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 import java.util.LinkedList; import java.awt.*; public class MonteCarloPiData { private Circle circle; private LinkedList<Point> points; private int insideCircle = 0; public MonteCarloPiData(Circle circle){ this.circle = circle; points = new LinkedList<Point>(); } public Circle getCircle(){ return circle; } public int getPointsNumber(){ return points.size(); } public Point getPoint(int i){ if(i < 0 || i >= points.size()) throw new IllegalArgumentException("out of bound in getPoint!"); return points.get(i); } public void addPoint(Point p){ points.add(p); if(circle.contain(p)) insideCircle ++; } public double estimatePi(){ if(points.size() == 0) return 0.0; int circleArea = insideCircle; int squareArea = points.size(); return (double)circleArea * 4 / squareArea; } }
一个可视化(View)相关类:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 import java.awt.*; import java.util.LinkedList; import javax.swing.*; public class AlgoFrame extends JFrame{ private int canvasWidth; private int canvasHeight; public AlgoFrame(String title, int canvasWidth, int canvasHeight){ super(title); this.canvasWidth = canvasWidth; this.canvasHeight = canvasHeight; AlgoCanvas canvas = new AlgoCanvas(); setContentPane(canvas); pack(); setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE); setResizable(false); setVisible(true); } public AlgoFrame(String title){ this(title, 1024, 768); } public int getCanvasWidth(){return canvasWidth;} public int getCanvasHeight(){return canvasHeight;} // data private MonteCarloPiData data; public void render(MonteCarloPiData data){ this.data = data; repaint(); } private class AlgoCanvas extends JPanel{ public AlgoCanvas(){ // 双缓存 super(true); } @Override public void paintComponent(Graphics g) { super.paintComponent(g); Graphics2D g2d = (Graphics2D)g; // 抗锯齿 RenderingHints hints = new RenderingHints( RenderingHints.KEY_ANTIALIASING, RenderingHints.VALUE_ANTIALIAS_ON); hints.put(RenderingHints.KEY_RENDERING, RenderingHints.VALUE_RENDER_QUALITY); g2d.addRenderingHints(hints); // 具体绘制 AlgoVisHelper.setStrokeWidth(g2d, 3); AlgoVisHelper.setColor(g2d, AlgoVisHelper.Blue); Circle circle = data.getCircle(); AlgoVisHelper.strokeCircle(g2d, circle.getX(), circle.getY(), circle.getR()); for(int i = 0 ; i < data.getPointsNumber() ; i ++){ Point p = data.getPoint(i); if(circle.contain(p)) AlgoVisHelper.setColor(g2d, AlgoVisHelper.Red); else AlgoVisHelper.setColor(g2d, AlgoVisHelper.Green); AlgoVisHelper.fillCircle(g2d, p.x, p.y, 3); } } @Override public Dimension getPreferredSize(){ return new Dimension(canvasWidth, canvasHeight); } } }
一个控制器(Controller):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 import java.awt.*; import java.util.LinkedList; import javax.swing.*; public class AlgoVisualizer { private static int DELAY = 40; private MonteCarloPiData data; private AlgoFrame frame; private int N; public AlgoVisualizer(int sceneWidth, int sceneHeight, int N){ if(sceneWidth != sceneHeight) throw new IllegalArgumentException("This demo must be run in a square window!"); this.N = N; Circle circle = new Circle(sceneWidth/2, sceneHeight/2, sceneWidth/2); data = new MonteCarloPiData(circle); // 初始化视图 EventQueue.invokeLater(() -> { frame = new AlgoFrame("Monte Carlo", sceneWidth, sceneHeight); new Thread(() -> { run(); }).start(); }); } public void run(){ for(int i = 0 ; i < N ; i ++){ if( i % 100 == 0) { frame.render(data); AlgoVisHelper.pause(DELAY); System.out.println(data.estimatePi()); } int x = (int)(Math.random() * frame.getCanvasWidth()); int y = (int)(Math.random() * frame.getCanvasHeight()); data.addPoint(new Point(x, y)); } } public static void main(String[] args) { int sceneWidth = 800; int sceneHeight = 800; int N = 20000; AlgoVisualizer vis = new AlgoVisualizer(sceneWidth, sceneHeight, N); } }
照旧使用了MVC框架,以下是GIF演出。
可视化后,因为加入了刷新屏幕的流程,总体的运算速度会慢一些。(当然可以先记录数据再刷新屏幕,但那需要占用额外的空间)
Tips:
在循环中,判断i % step == 0,以 step作为输出步长(每step次输出一次)。
在屏幕刷新前,进行数据处理的时候,可以在前面加上for循环x次,使得数据处理x次后再刷新屏幕。可以加速数据的处理。
三门问题 “三门问题”也叫“蒙提霍尔问题”(Monty Hall Problem),是一个有关于博弈论的趣味数学问题。
三门问题的主要内容表述如下:在这个电视节目中有三扇门,这三扇门的后面会被随机的放进去物品,物品分别是汽车和两只山羊,此时参赛者要随机选择一扇门,在参赛者选择了一扇门之后,主持人并不会立刻打开这扇门,为了制造节目紧张悬疑的气氛,支持人会从剩下的两扇门中打开一扇有山羊的那扇门,随后主持人会给竞猜者提供一次重新选择门的机会,此时竞猜者可以保持自己的第一选择不变,也可以更换自己的选择选择另外一扇门,那么参赛者到底是应该换门呢?还是不换门呢?怎么样做得到汽车大奖的概率大一些呢?
不错,我叛逃了java swing,以下结果由unity模拟:
unity模拟三门问题 - 白序的视频 - 知乎